Fill out row 4 of Pascal’s Triangle.
Solution.
Following the same process, row 4 has entries \(1, (1+3), (3+3), (3+1), 1 \) or \(1, 4, 6, 4, 1\text{.}\)
Section 2.2 A Special Triangle
Subsection 2.2.1 Introduction
You can find all sorts of interesting examples of surprising structures in the universe of mathematics. One such example is a very special triangle of numbers that’s easy to construct and borderline ubiquitous in its applications.
This triangle goes by many names and was discovered by several cultures in history. In 450 BC, Indian mathematician, Pingata, called this new construction the "Staircase of Mount Meru". Persian mathematician, Omar Khayyam, discovered "Khauuam’s Triangle" in the 11th century, and close to the same time, Chinese mathematician, Jin Xian, discovered "Yang Hui’s Triangle". In the western world, this triangle is most commonly refered to as Pascal’s Triangle, named after french mathematician, Blaise Pascal, who discovered this triangle in the 17th century. REFERENCE
Subsection 2.2.2 Constructing Pascal’s Triangle
Now we will follow the foot steps of giants. We can build Pascal’s Triangle by listing out the rows. For the first row (row \(0\)), we just write \(1\text{,}\) and the second row is composed of \(1, 1\text{.}\) The third row (what we call row 2) consists of \(1, 2
, 1\) like below.
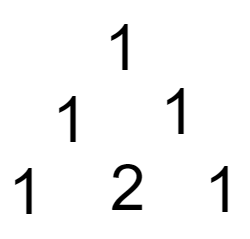
The pattern of Pascal’s Triangle is not immediately obvious for us yet. The \(2\) in row 2 comes from adding the two \(1\)’s above it in row 1. For the next row (row 3), we start with \(1\text{.}\) The next entry consists of the sum of the two numbers above it (\(1 + 2\)). Next is the sum \(2+1\text{,}\) and finally we end the row with \(1\text{.}\) That is, row 3 is \(1, 3, 3, 1\text{.}\)
Then we just repeat this process.
Question 2.2.4. Row 4.
Activity 2.2.1.
Subsection 2.2.3 Patterns of Pacal’s Triangle
Pascal’s triangle has interested mathematicians for centuries, as it is filled with interesting patterns.
Question 2.2.5. Adding along a row.
Add entries of rows 0 through 4. What pattern do you notice?
Solution.
The sume of entries of rows 0 through 4 are \(1, 2, 4, 8, 16\) respectively. These looks like powers of \(2\text{.}\)
We just uncovered that the sum of entries along row \(n\) add up to \(2^n\text{.}\) This is just one pattern of Pascal’s triangle, but there are many more. Wadji Mohamed Retemi expertly hightlights some of these patterns we find in Pascal’s triangle in this Ted Ed video.
Use TedEd’s video and Pascal’s Triangle to answer the following.
Question 2.2.7. Binomial Expansion.
Use Pascal’s Triangle to expand the binomial \((x+y)^4. \)
Question 2.2.8. Powers of 11.
Use Pascal’s Triangle to find \(11^7. \)
Question 2.2.9. Counting Apples.
There are \(6\) apples on a counter. In how many ways could we select \(4\) of them? Use Pascal’s Triangle to decide.
Question 2.2.10. Triangular Numbers.
List out of the first 6 triangular numbers.
Question 2.2.11. Tetrahedral Numbers.
What is the 5th tetrahedral number?
