If you were born sometime after the mid-80’s, chances are you have played a popular game featuring a pair of Italian plumbers. Something about pipes.
Imagine a pipe network like the one in Figure 4.1.1. In this figure, we mark the volume of water moving across these pipes over a given period of time (we call that the flow rate) as well as the direction of flow along the pipes. As you can see, we can measure the flow rate on some of the pipes, but not all of them. But we would really like to know the how much water is passing through all of them.
Figure4.1.1.
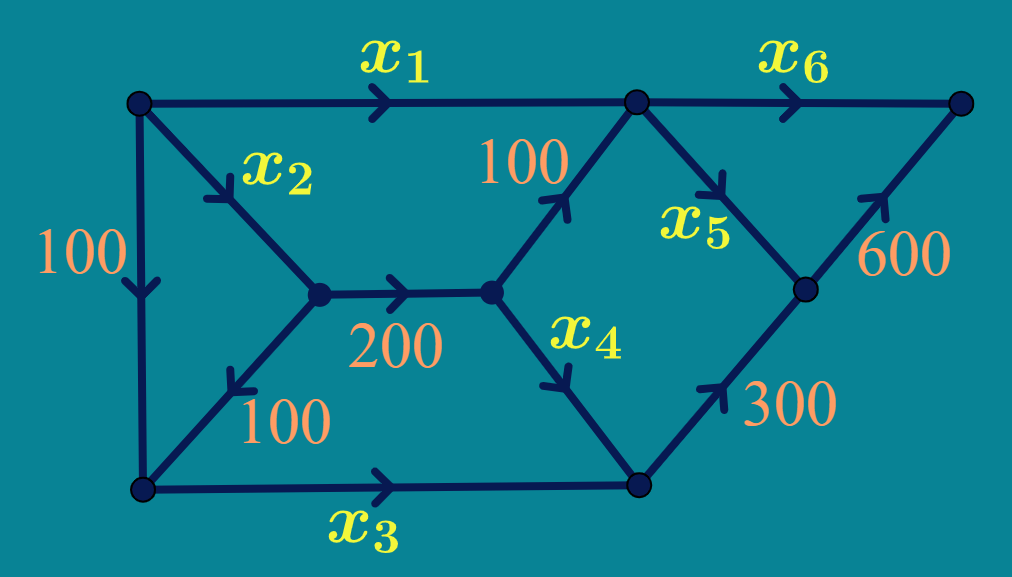
At each intersection point, you might notice there are some pipes flowing into that point and others flowing out. Actually, that observation might give us some insight.
Question4.1.2.
Suppose we know that 100 cubic meters of water is flowing into one intersection point. How much water is flowing out of that intersection point?
Solution.
The water can’t stay at the intersection point, so 100 cubic meters is flowing out from that point.
We now know that at a given intersection point, the total that flows into the intersection is the same as the total flow that flows out from that intersection point. This introduces an equation! This principle is referred to Kirchoff’s Law of Flow.
So our question is, "What possible values along the pipes marked \(x_1\) through \(x_6\) satisfy Kirchoff’s Law of Flow?" If we can answer this question, then we will know all of the flowrates along our pipe system.
